Diện tích toàn phần hình hộp chữ nhật là tổng diện tích 6 mặt, thường gây khó khăn cho học sinh lớp 5. Công thức đơn giản: S_toàn phần = 2ab + 2(a + b)h (với a: chiều dài, b: chiều rộng, h: chiều cao). Bài viết hướng dẫn chi tiết định nghĩa, tính chất, công thức tính diện tích xung quanh và toàn phần, kèm ví dụ, bài tập thực hành để bạn dễ dàng áp dụng.
Đôi nét về hình hộp chữ nhật
Như đã trình bày, để áp dụng thành công cách tính diện tích hình hộp chữ nhất thì trước hết bạn phải nắm bắt được định nghĩa và tính chất của hình học không gian này. Dưới đây là gợi ý về vấn đề này mà bạn có thể tham khảo.
Định nghĩa
Hình hộp chữ nhật là một dạng hình không gian cơ bản và khá quen thuộc trong toán học. Cụ thể, đây là một loại hình hộp có sáu mặt, trong đó các mặt đối diện có đặc điểm song song và bằng nhau. Điều này tạo nên các góc vuông tại đặc biệt tại các đường thẳng giao nhau. Chẳng hạn, hộp đựng phấn có thể là một hình hộp chữ nhật mà bạn có thể gặp thường xuyên trong môi trường học đường.
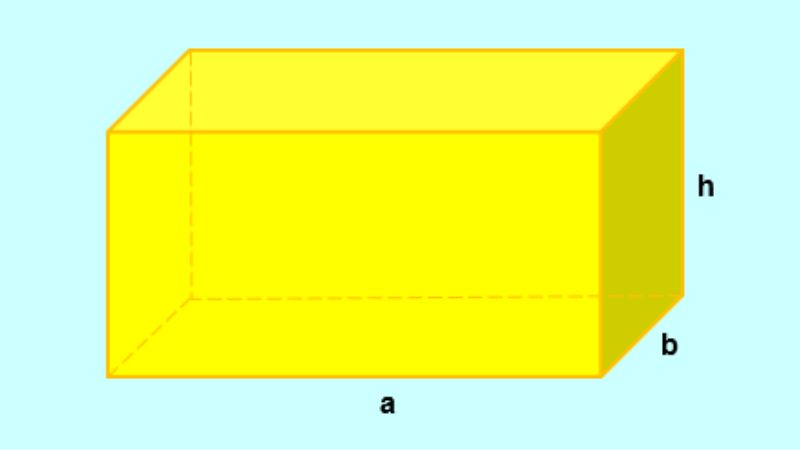
Ngoài ra, bạn cũng có thể dễ dàng nhìn thấy hình hộp chữ nhật thường xuất hiện trong nhiều tình huống thực tế như đóng gói sản phẩm, xây dựng công trình, thiết kế nội thất và nhiều ứng dụng khác. Trong đó, công thức tính diện tích hình hộp chữ nhật không chỉ giúp người dùng hiểu rõ về hình dạng hình học mà còn áp dụng vào nhiều vấn đề thực tế, từ quy hoạch đô thị đến sản xuất và kỹ thuật. Điều này thể hiện sự quan trọng và ảnh hưởng sâu rộng của hình học không gian này trong cuộc sống của con người.
Tính chất
Hình hộp chữ nhật là một dạng hình học không gian sở hữu nhiều đặc tính độc đáo mà bạn có thể tham khảo như:
- Trong hình hộp chữ nhật, hai mặt đối xứng sẽ luôn luôn có S bằng nhau. Bởi lẽ, chúng được tạo đối xứng và sở hữu các cạnh có độ dài bằng nhau.
- Không chỉ diện tích, chu vi của các mặt đối diện trong hình học đặc biệt này cũng bằng nhau. Tính chất này giúp cho người dùng dễ dàng tính được độ dài và diện tích hình hộp chữ nhật.
- Hình hộp chữ nhật có tổng cộng 12 cạnh, 6 mặt và 8 đỉnh. Tính chất này thể hiện cấu trúc độc đáo và phức tạp của hình hộp chữ nhật. Đồng thời làm cho loại hình học này trở thành một đối tượng được sử dụng phổ biến trong nhiều lĩnh vực.
- Đường chéo trong hình hộp chữ nhật là các đoạn thẳng nối liền hai đỉnh không kề nhau. Chúng giao nhau cùng một điểm và tạo nên một mối liên kết đặc biệt giữa các mặt của hình hộp.
Cách tính chi tiết diện tích hình hộp chữ nhật
Các tính diện tích hình hộp chữ nhật không đơn giản như chúng ta nghĩa. Bởi lẽ, công thức tính diện tích hình học này khá phức tạp và gồm nhiều yếu tố cấu thành như diện tích xung quanh và diện tích đáy. Cụ thể, bạn có thể tham khảo hướng dẫn dưới đây để nắm bắt được cách tính của chúng tôi.
Diện Tích Xung Quanh Hình Hộp Chữ Nhật
Diện tích xung quanh là tổng diện tích 4 mặt bên (không tính 2 đáy):
S_xq = 2(a + b) × h
Diện Tích Toàn Phần Hình Hộp Chữ Nhật
Diện tích toàn phần là tổng diện tích 6 mặt:
Stp = Sxq + 2 × Sđáy = 2ab + 2(a + b)h
(Lưu ý: Chu vi đáy P = 2(a + b), Sđáy = a × b)
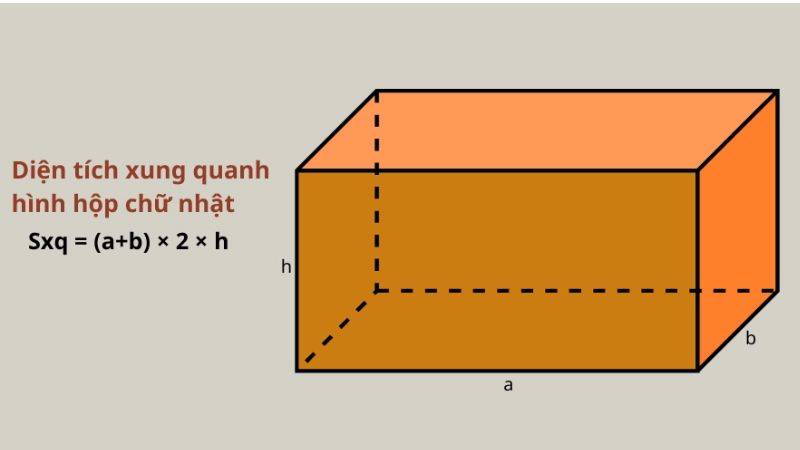
Như vậy, Sxung quanh của hình hộp chữ nhật sẽ được tính bằng công thức như sau:
Sxung quanh = 2 (a + b) x h
Diện tích toàn phần hình hộp chữ nhật
Diện tích toàn phần của hình hộp chữ nhật là tổng diện tích của tất cả các mặt, bao gồm các mặt bên và mặt đáy. Hiểu đơn giản, đây là diện tích xung quanh và diện tích đáy của hình học không gian này. Theo đó, đó nếu chúng ta vẫn giả sử chiều dài của hình hộp này là a, chiều rộng là b và chiều cao là h thì diện tích đáy sẽ bằng 2ab.
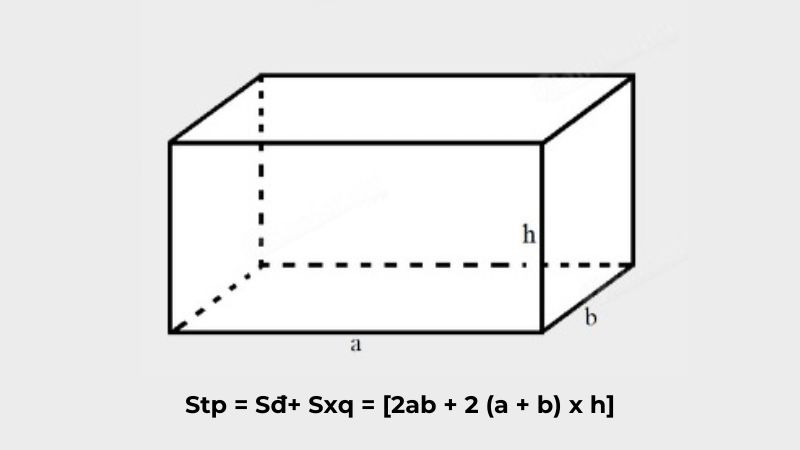
Từ đó, công thức tính diện tích hình hộp chữ nhất sẽ được biểu diễn chi tiết như sau:
Stoàn phần = Sđáy+ Sxung quanh = [2ab + 2 (a + b) x h]
Ví dụ minh họa về cách tính diện tích hình hộp chữ nhật
Để nắm bắt và triển khai được các công thức tính S của hình hộp chữ nhật bên trên, bạn hãy cùng chúng tôi thử một số dạng bài toán sau đây nhé.
Ví Dụ 1 (Cơ Bản)
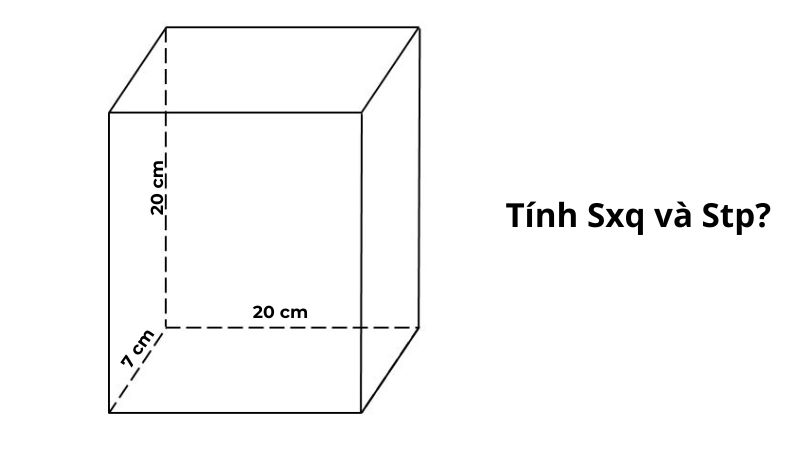
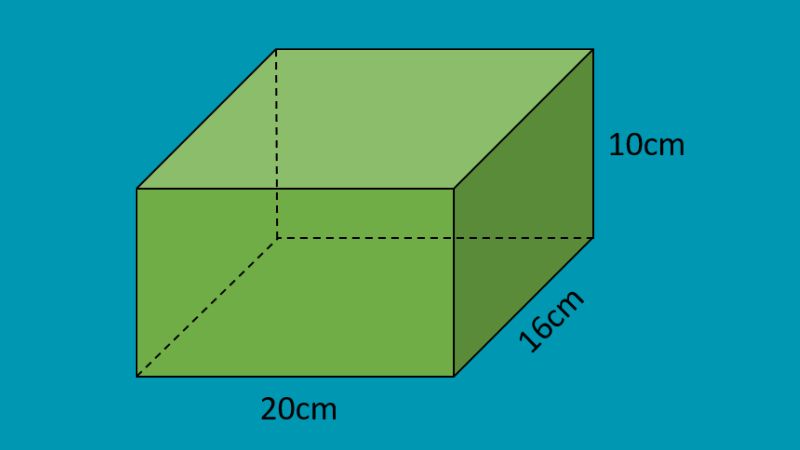
Hình hộp chữ nhật: a=20cm, b=7cm, h=20cm.
Sxq = 2(20+7)×20 = 540 cm² Stp = 2×20×7 + 540 = 820 cm²
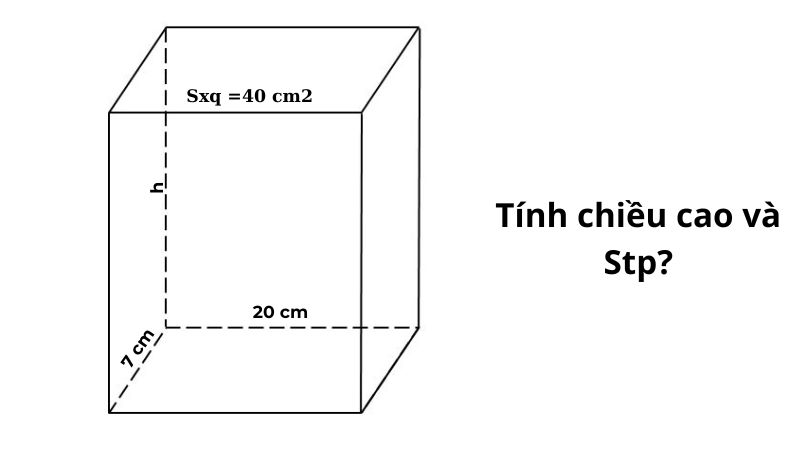
Ví Dụ 2 (Nâng Cao – Tìm Chiều Cao)
Cho a=20cm, b=7cm, Sxq=540 cm². Tính h và Stp.
h = 540 / [2(20+7)] = 20 cm
S_tp = 2×20×7 + 540 = 820 cm²
Lời giải:
Từ công thức tính diện tích xung quanh, ta có:
Sxung quanh = 2 (a + b) x h => h = Sxung quanh : [2 (a + b)] = 540 : [2 (20 + 7)] = 20 cm
Như vậy, chiều cao cần tìm của hình hộp chữ nhật này đó là 20 cm. Do đó, Stp của hình hộp chữ nhật trên sẽ được vận dụng dễ dàng theo công thức sau:
Stoàn phần = [2ab + 2 (a + b) x h] = [2 x 20 x 7 + 2 (20 +7) x 20] = 820 cm2
Đáp số: 820 cm2
Ví Dụ 3 (Bài Tập Lớp 5): Hộp không nắp: a=30cm, b=20cm, h=15cm. Tính diện tích tôn (Sxq + Sđáy). Kết quả: 2100 cm².
Những lưu ý khi tính diện tích hình hộp chữ nhật
Khi tính S của hình hộp chữ nhật, có một số điểm quan trọng mà người dùng cần lưu ý để đảm bảo tính chính xác và hiểu rõ về bài toán như sau:
- Để tính diện tích hình hộp chữ nhật, bạn cần xác định chính xác độ dài kích thước của chiều dài (a), chiều rộng (b) và chiều cao (h) để tránh sai sót trong quá trình tính toán.
- Chắc chắn rằng tất cả các kích thước trong hình hộp chữ hiển thị cùng một đơn vị. Nếu các đơn vị khác nhau, hãy chuyển đổi chúng thành cùng một đơn vị trước khi tính toán.
- Sau khi tính diện tích, hãy kiểm tra lại kết quả của bạn để đảm bảo tính chính xác. Đôi khi, một lỗi nhỏ trong việc đọc số liệu hoặc thực hiện phép tính có thể dẫn đến kết quả không chính xác.
- Hiểu rõ các ngữ cảnh và yêu cầu của bài toán đặt ra. Điều này giúp xác định diện tích nào cần được tính toán (xung quanh, toàn phần) và cách sử dụng kết quả tính toán trong ngữ cảnh cụ thể của vấn đề.
- Trong nhiều trường hợp số liệu quá nhiều, bạn có thể sử dụng máy tính hoặc công cụ tính toán trực tuyến có thể giúp giảm thiểu sai số tính toán và tăng tính chính xác trong quá trình giải.
Ứng dụng của công thức tính diện tích hình hộp chữ nhật
Công thức tính diện tích hình hộp chữ nhật thực tế đóng vai trò đặc biệt đối với nhiều lĩnh vực, đặc biệt là trong khía cạnh học tập. Việc liên tục xuất hiện trong các đề thi quốc gia khiến cho công thức này trở thành một chủ đề được nhiều học sinh chú trọng nghiên cứu. Điều này tác động rất lớn đến chất lượng đào tạo trong lĩnh vực giáo dục. Đồng thời trang bị cho học sinh những kỹ năng cần thiết trong việc tính toán và làm việc trong môi trường hình học không gian đa chiều.

Hơn thế, trong lĩnh vực xây dựng và kiến trúc, công thức này được ứng dụng để tính toán lượng vật liệu cần thiết cho việc xây dựng các cấu trúc như tường, sàn và mái nhà. Nó cũng hỗ trợ trong việc đưa ra bảng báo giá và ước lượng chi phí xây dựng. Thậm chí, nhiều người còn áp dụng cách tính diện tích hình hộp chữ nhật để xác định bề mặt của sản phẩm. Từ đó giúp họ dễ dàng đưa ra quyết định liên quan đến lượng vật liệu bao bì cần sử dụng và thời gian hoàn thành lượng công việc được giao.
Ngoài ra, công thức tính S của hình hộp chữ nhật còn được áp dụng trong nhiều lĩnh vực khác nhau. Chúng có vai trò quan trọng trong ngành thiết kế đồ họa, lĩnh vực bất động sản, quy hoạch đô thị,… Do đó, việc hiểu và áp dụng cách tính của hình học không gian này là điều cần thiết mà mọi học sinh đều phải nắm bắt được.
Những thắc mắc chung khi tính diện tích hình hộp chữ nhật
Nếu trong quá trình áp dụng công thức tính hình hộp chữ nhật của bạn cũng gặp vấn đề, hãy tham khảo một số phương án đề xuất của chúng tôi dưới đây nhé.
Nên tính diện tích toàn phần của hình hộp chữ nhật khi nào?
Trả lời: Thực tế, đối với các bài toán thì học sinh nên tính diện tích hình hộp chữ nhật khi tìm hiểu các chỉ số về chiều dài, chiều rộng và chiều cao. Hiểu chi tiết hơn, người dùng nên tính Stp của hình hộp chữ nhật khi bạn cần có thông tin về tổng diện tích của tất cả các mặt bao gồm cả mặt đáy và mặt trên, cùng với tất cả các mặt bên của khối hộp.
Tính diện tích xung quanh hình hộp chữ nhật để làm gì?
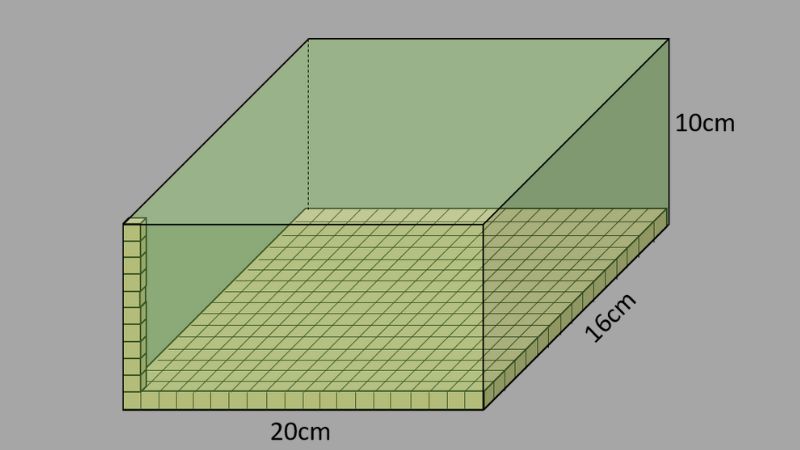
Trả lời: Thường thì việc tính diện tích xung quanh có mục đích chính là để đo lường phần bề mặt nằm xung quanh hình hộp. Điều này hay được ứng dụng trong việc sơn, lót hoặc đóng gói vật phẩm nhằm giúp ước lượng lượng vật liệu cần thiết và chi phí liên quan mà không cần xét đến mặt đáy và mặt trên của hình hộp chữ nhật.
Nhìn chung, công thức tính diện tích hình hộp chữ nhật được ứng dụng rất nhiều trong cuộc sống của chúng ta. Do đó, Hoàng Hà Mobile mong rằng, quý độc giả khi đã nghiên cứu về định nghĩa và tính chất cũng như công thức của hình học này thì sẽ áp dụng được chúng trong quá trình làm việc và học tập của mình. Đừng quên, cập nhật thêm các gợi ý dưới đây để bổ sung vào kho tàng kiến thức cá nhân của mình nhé.
XEM THÊM