Công thức đạo hàm có vai trò quan trọng và mạnh mẽ của lĩnh vực toán học. Nó không chỉ có giá trị lý thuyết mà còn mang lại ảnh hưởng lớn trong nhiều lĩnh vực ứng dụng. Trong bài viết này, chúng ta sẽ khám phá cẩm nang về các công thức của đạo hàm, từ những phương pháp cơ bản đến những ứng dụng thực tế của chúng. Đồng thời chúng ta sẽ đi sâu vào những phương pháp tính đạo hàm phổ biến, khám phá các ví dụ thực tế và ứng dụng hấp dẫn bạn nhé.
Công thức đạo hàm là gì?
Công thức đạo hàm là một công cụ toán học quan trọng trong việc tính toán độ dốc của một đường cong tại một điểm cụ thể. Đạo hàm của một hàm số f(x) tại điểm x=a được ký hiệu là f'(a) hoặc đơn giản là f'(x). Đạo hàm cũng cung cấp thông tin về độ dốc của đồ thị hàm số tại mỗi điểm. Nếu đạo hàm dương tại một điểm, hàm số tăng; nếu đạo hàm âm, hàm số giảm; nếu đạo hàm bằng 0, hàm số có điểm cực trị. Đạo hàm của một hàm số có thể được tính bằng nhiều phương pháp khác nhau, nhưng công thức cơ bản nhất là:
Công thức của đạo hàm cơ bản của một số hàm số phổ biến như sau:
- Đạo hàm của hàm số hằng: f(x) = c, với c là một hằng số, đạo hàm của f(x) là f'(x) = 0.
- Đạo hàm của hàm số mũ: f(x) = x^n, với n là một số nguyên dương, đạo hàm của f(x) là f'(x) = nx^(n-1).
- Đạo hàm của hàm số mũ tự nhiên: f(x) = e^x, đạo hàm của f(x) là f'(x) = e^x.
- Đạo hàm của hàm số sin và cos: f(x) = sin(x), f'(x) = cos(x); f(x) = cos(x), f'(x) = -sin(x).
Ngoài ra, còn có nhiều công thức về đạo hàm khác cho các loại hàm số khác nhau như hàm số hợp, hàm số mũ, hàm số lượng giác, hàm số mũ, và nhiều loại hàm số phức tạp khác.
Ý nghĩa của công thức đạo hàm
Trong lĩnh vực vật lý, công thức của đạo hàm được sử dụng để tính toán vận tốc, gia tốc và các đại lượng khác trong quá trình di chuyển của vật thể. Đạo hàm cho biết tốc độ thay đổi của một hàm số tại mỗi điểm. Điều này rất hữu ích trong việc hiểu sự biến đổi của các hiện tượng trong thế giới thực. Từ tốc độ di chuyển của vật thể đến tốc độ tăng trưởng của dân số hay tốc độ thay đổi của giá cả.
Trong kinh tế học, đạo hàm được sử dụng để tối ưu hóa hàm lợi nhuận và tìm ra điểm cực đại hoặc cực tiểu của hàm số. Công thức của đạo hàm được sử dụng trong tối ưu hóa, nơi mà chúng ta cố gắng tìm ra giá trị lớn nhất hoặc nhỏ nhất của một hàm số. Bằng cách sử dụng đạo hàm, chúng ta có thể xác định các điểm cực trị và điểm uốn của hàm số. Từ đó giúp tối ưu hóa các vấn đề thực tế như tối ưu hóa chi phí, tối ưu hóa hiệu suất, v.v.
Đạo hàm còn giúp chúng ta hiểu rõ hơn về tính chất của hàm số, bao gồm đồ thị, điểm cực trị, điểm uốn, và xu hướng tăng hoặc giảm của hàm số.
Đạo hàm được sử dụng rộng rãi trong các lĩnh vực khoa học và kỹ thuật như vật lý, kỹ thuật điện, kỹ thuật hóa học, khoa học máy tính, kinh tế học, v.v.
Các công thức đạo hàm
Sau khi hiểu rõ được ý nghĩa của đạo hàm là gì. Chúng ta sẽ đi đến phần công thức của các loại đạo hàm nhé.
Công thức đạo hàm sơ cấp
Công thức đạo hàm cấp cao
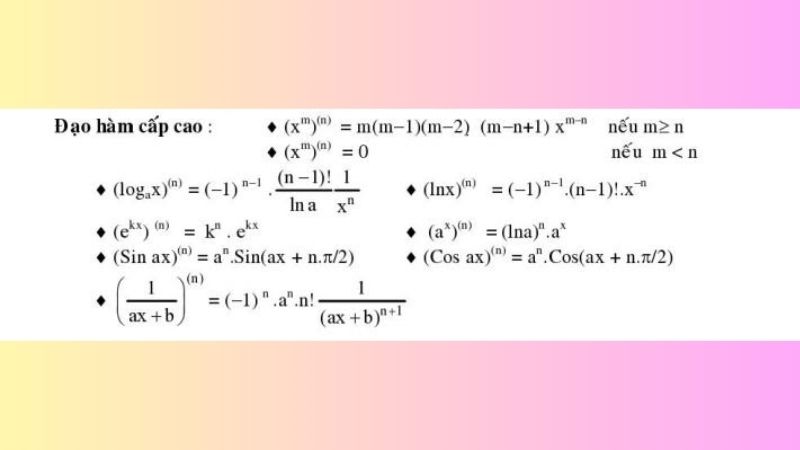
Công thức đạo hàm lượng giác
Nhớ rằng, có nhiều quy tắc khác nhau, chẳng hạn như quy tắc chuỗi, quy tắc nhân, và quy tắc chia, để tính đạo hàm của các hàm phức tạp hơn.
Ví dụ cách tính đạo hàm
Có nhiều phương pháp để tính đạo hàm của một hàm số. Mỗi phương pháp có cách áp dụng riêng. Và chúng ta sẽ đi sâu vào từng phương pháp để giúp các bạn hiểu rõ hơn về cách tính đạo hàm.
Cách tính đạo hàm của hàm số mũ
Hàm số mũ được biểu diễn dưới dạng f(x) = a^x, với a là một hằng số dương. Đạo hàm của hàm số mũ được tính bằng công thức sau: f'(x) = a^x * ln(a).
Trong đó, ln(a) là logarit tự nhiên của a. Ví dụ, để tính đạo hàm của hàm số f(x) = 2^x, ta áp dụng công thức trên và có: f'(x) = 2^x * ln(2).
Cách tính đạo hàm của hàm số logarit
Hàm số logarit tự nhiên được biểu diễn dưới dạng f(x) = ln(x). Công thức đạo hàm của hàm số logarit được tính như sau: f'(x) = 1/x
Ví dụ, để tính đạo hàm của hàm số f(x) = ln(x), ta áp dụng công thức trên và có: f'(x) = 1/x
Hàm số lượng giác có thể là sin(x), cos(x), hoặc tan(x). Đạo hàm của hàm số sin(x) và cos(x) được tính bằng công thức sau: f'(x) = cos(x) (nếu f(x) = sin(x)) f'(x) = -sin(x) (nếu f(x) = cos(x))
Đạo hàm của hàm số tan(x) được tính như sau: f'(x) = sec^2(x)
Trong đó, sec(x) là hàm số secant, được định nghĩa là sec(x) = 1/cos(x). Ví dụ, để tính đạo hàm của hàm số f(x) = sin(x), ta áp dụng công thức trên và có: f'(x) = cos(x)
Cách tính đạo hàm của hàm số hợp
Hàm số hợp là hàm số được tạo thành bằng cách kết hợp các hàm số khác với nhau. Đạo hàm của hàm số hợp được tính bằng quy tắc chuỗi (chain rule). Quy tắc chuỗi nói rằng đạo hàm của hàm số hợp f(g(x)) được tính bằng tích giữa đạo hàm của hàm số ngoài f và đạo hàm của hàm số trong g.
Ví dụ, để tính đạo hàm của hàm số f(x) = sin(2x), ta áp dụng quy tắc chuỗi và có: f'(x) = cos(2x) * 2
Trong đó, công thức đạo hàm của hàm số ngoài f là cos(x), và đạo hàm của hàm số trong g là 2x (vì g(x) = 2x). Do đó, tích giữa hai đạo hàm này là cos(2x) * 2.
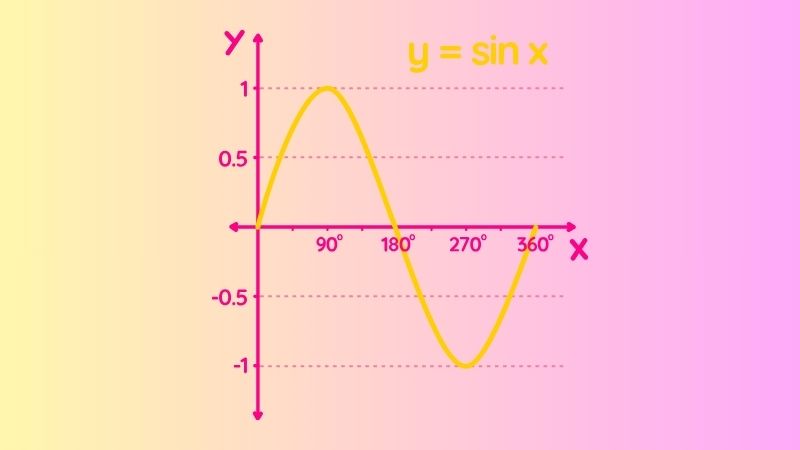
Như vậy, qua các ví dụ trên, chúng ta đã thấy được cách tính đạo hàm của các hàm số phổ biến và cách áp dụng chúng trong thực tế. Việc hiểu rõ về đạo hàm và cách áp dụng chúng sẽ giúp chúng ta giải quyết các bài toán liên quan đến tốc độ, gia tốc, tối ưu hóa và nhiều lĩnh vực khác.
Minh họa về công thức đạo hàm
Để bạn có thể hình dung được đạo hàm dùng để làm gì cũng như đạo hàm được ứng dụng ra sao. Cùng mình đọc hết mục này để hiểu rõ hơn nhé.
Tính tốc độ và gia tốc
Trong vật lý, đạo hàm được sử dụng để tính toán tốc độ và gia tốc của vật thể. Tốc độ của một vật thể có thể được xác định bằng đạo hàm của vị trí theo thời gian. Trong khi gia tốc có thể được tính bằng đạo hàm của tốc độ theo thời gian.
Ví dụ: Nếu vị trí của một vật thể được mô tả bởi hàm số s(t) = 5t^2 – 3t + 2. Thì vận tốc của vật thể tại thời điểm t=a có thể được tính bằng đạo hàm của hàm số s(t) tại t=a, tức là s'(a).
Một ví dụ cụ thể về việc áp dụng công thức đạo hàm là trong vật lý. Khi một vật thể di chuyển theo một đường cong. Chúng ta có thể sử dụng đạo hàm để tính toán vận tốc của vật thể tại một thời điểm cụ thể. Vận tốc của vật thể có thể được xác định bằng đạo hàm của hàm số vị trí theo thời gian.
Tối ưu hoá
Trong kinh tế học và kỹ thuật, đạo hàm được sử dụng để tối ưu hóa các hàm mục tiêu. Bằng cách tìm đạo hàm của hàm mục tiêu và đặt nó bằng 0, chúng ta có thể tìm ra giá trị tối ưu của biến số.
Chúng ta sẽ cung cấp một số ví dụ cụ thể về cách tính đạo hàm của các hàm số phổ biến. Như hàm số mũ, hàm số logarit, hàm số lượng giác, và hàm số hợp.
Mô phỏng các tình huống thực tế bằng cách sử dụng đạo hàm
Mô phỏng các tình huống thực tế bằng cách sử dụng đạo hàm là một phương pháp quan trọng để hiểu và giải quyết các vấn đề trong nhiều lĩnh vực khác nhau.
Với chuyển động và vận tốc
Giả sử chúng ta muốn mô phỏng chuyển động của một vật thể dựa trên hàm vị trí theo thời gian. Bằng cách lấy đạo hàm của hàm vị trí đó. Chúng ta có thể tính được vận tốc của vật thể tại mọi thời điểm.
Tối ưu hóa chi phí sản xuất
Trong kỹ thuật và quản lý sản xuất, việc tối ưu hóa chi phí là quan trọng. Công thức đạo hàm có thể được sử dụng để tìm ra giá trị cực tiểu của hàm chi phí, giúp tối ưu hóa quy trình sản xuất.
Dự đoán xu hướng tài chính
Đạo hàm có thể được sử dụng để mô phỏng biến động của giá cổ phiếu. Việc này giúp dự đoán xu hướng thị trường và hỗ trợ quyết định giao dịch.
Tối ưu hóa mạng neuron trong Machine Learning
Trong deep learning, việc cập nhật trọng số của mạng neuron dựa trên đạo hàm của hàm mất mát giúp tối ưu hóa mô hình và cải thiện hiệu suất dự đoán.
Ứng dụng trong sinh học
Đạo hàm cũng có thể được sử dụng để mô phỏng sự biến đổi của dữ liệu sinh học. Chẳng hạn như tốc độ tăng trưởng của một loại vi khuẩn trong một môi trường cụ thể.
Tối ưu hóa tiêu thụ năng lượng trong IoT
Trong Internet of Things (IoT), đạo hàm có thể được áp dụng để tối ưu hóa tiêu thụ năng lượng của thiết bị thông minh, giúp gia tăng hiệu suất và tuổi thọ pin.
Cách ghi nhớ công thức đạo hàm lâu
Đầu tiên, hãy hiểu cơ bản về lý thuyết đằng sau các công thức đạo hàm. Nếu bạn hiểu ý nghĩa của nó, việc nhớ nó sẽ dễ dàng hơn. Lặp lại công thức nhiều lần có thể giúp não bộ của bạn ghi nhớ chúng. Việc làm này giúp tăng cường bộ nhớ dài hạn.
Nhóm các đạo hàm dựa trên tính chất chung của chúng. Ví dụ, nhóm các công thức cho hàm số mũ, logarit, lượng giác, để nhớ chúng dễ dàng hơn. Áp dụng các công thức đạo hàm vào bài toán thực tế có thể giúp bạn liên kết chúng với ứng dụng cụ thể và dễ nhớ hơn.
Giải nhiều bài tập sử dụng các công thức ấy. Thực hành là một cách hiệu quả để ghi nhớ và làm quen với các công thức trong nhiều ngữ cảnh khác nhau.
Kết luận
Đạo hàm không chỉ là một phần quan trọng trong lĩnh vực toán học mà còn ảnh hưởng sâu rộng trong nhiều lĩnh vực ứng dụng. Chúng ta đã tìm hiểu về các công thức đạo hàm cơ bản. Nó bao gồm đạo hàm của hàm số hằng, hàm số mũ, hàm số logarit, hàm số lượng giác, và cách tính đạo hàm của các hàm số hợp. Những ứng dụng thực tế của đạo hàm mở ra những khả năng mới trong nhiều lĩnh vực. Đồng thời chứng minh sức mạnh và tính linh hoạt của nó trong việc giải quyết các vấn đề đa dạng và phức tạp.
Xem thêm:
