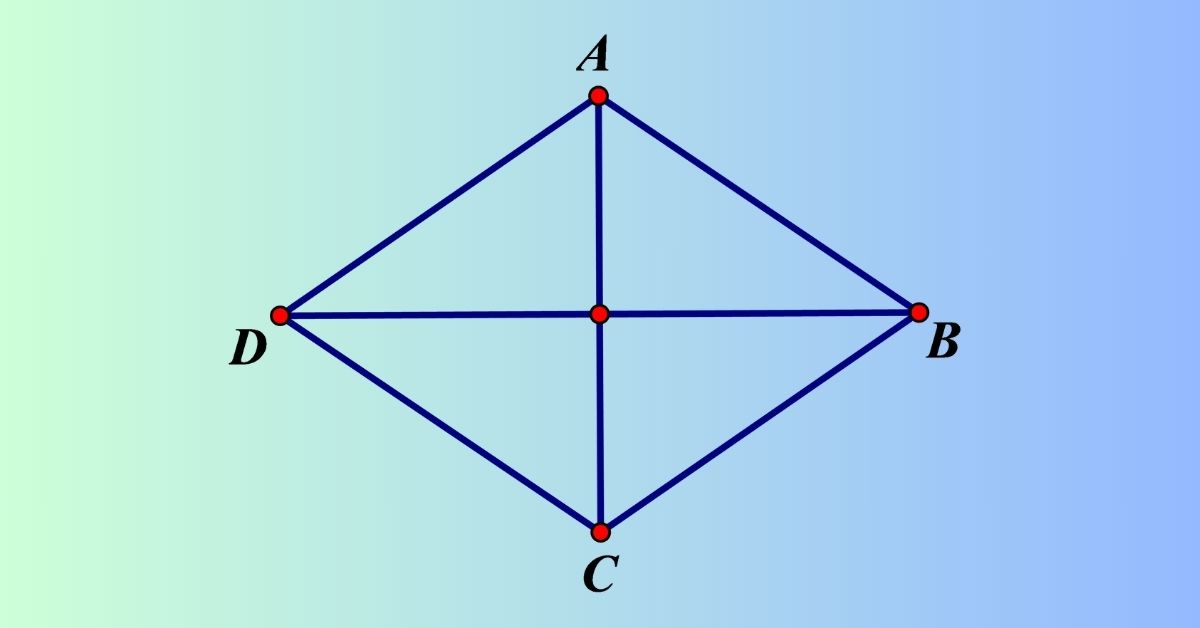
Chu vi hình thoi là một trong những kiến thức Toán học cơ bản và quan trọng, xuất hiện thường xuyên trong chương trình học phổ thông và các bài toán thực tế. Tuy nhiên, không phải ai cũng nắm vững tất cả các công thức và dạng bài tập liên quan.
Trong bài viết này, Hoàng Hà Mobile sẽ cùng bạn hệ thống lại toàn bộ kiến thức từ A-Z: từ định nghĩa, tính chất, công thức tính chu vi hình thoi trong mọi trường hợp, cho đến các dạng bài tập có lời giải chi tiết để bạn dễ dàng ôn tập và áp dụng.
Dấu hiệu nhận biết hình thoi
Để nhận biết một tứ giác có phải là hình thoi hay không, bạn có thể dựa vào các dấu hiệu sau:
- Tứ giác có bốn cạnh bằng nhau là hình thoi.
- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
- Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
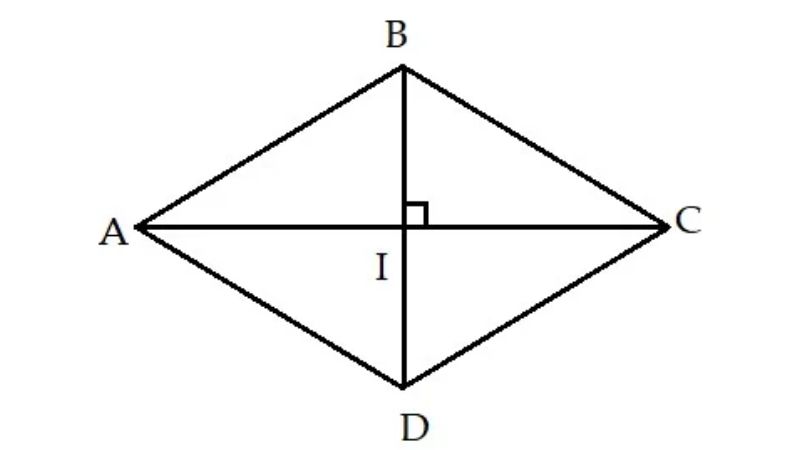
Hình thoi có tính chất nào?
Trước khi tìm hiểu chu vi hình thoi thì mọi người cần tìm hiểu dạng hình học này có tính chất như thế nào? Sau đây là vài tính chất trong hình thoi:
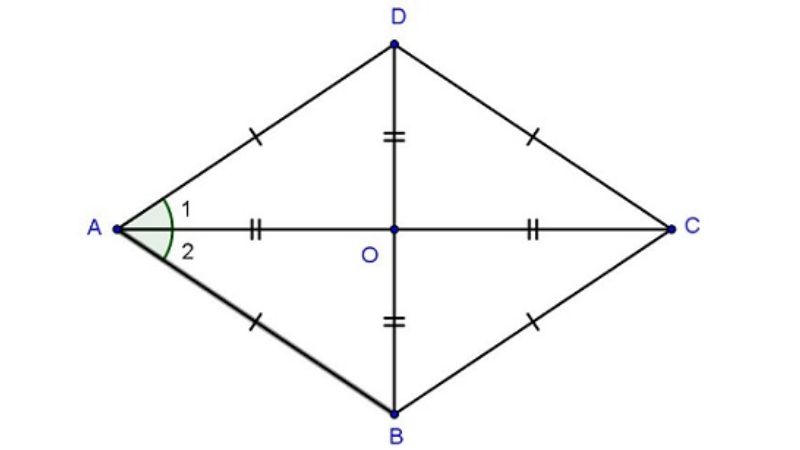
- Hình thoi gồm tất cả những tính chất có trong hình bình hành. Chẳng hạn như tính chất có những cạnh đối bằng nhau và song song cùng nhau, tính chất có những góc đối với số độ bằng nhau, 2 đường chéo trong hình cắt nhau ở trung điểm từng đường.
- Hình thoi bao gồm những góc đối có số độ như nhau, tổng tất cả các góc của hình thoi = 360 độ.
- Hình thoi gồm 2 đường chéo cắt nhau ở trung điểm từng đường và vuông góc.
- Hình thoi gồm 2 đường chéo được coi như đường phân giác tất cả các góc của hình thoi.
Công thức tính chu vi hình thoi và các dạng bài tập phổ biến
Về cơ bản, công thức tính chu vi hình thoi rất đơn giản. Chúng ta sẽ đi từ công thức gốc đến các dạng bài tập mở rộng thường gặp.
Dạng 1: Tính chu vi khi biết độ dài cạnh
Đây là dạng bài tập cơ bản nhất. Vì hình thoi có 4 cạnh bằng nhau, ta chỉ cần lấy độ dài một cạnh nhân với 4.
P = a x 4
Trong đó:
- P: là chu vi hình thoi.
- a: là độ dài một cạnh của hình thoi.
Ví dụ: Một hình thoi có độ dài cạnh là 7cm. Hỏi chu vi của hình thoi đó là bao nhiêu?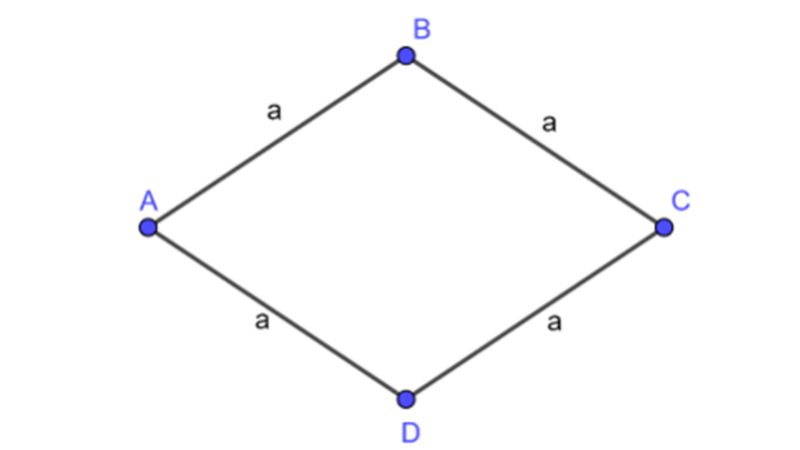
Lời giải: Áp dụng công thức, ta có chu vi hình thoi là: P = 7 x 4 = 28 (cm).
Dạng 2: Tính độ dài cạnh khi biết chu vi
Đây là bài toán ngược của dạng 1. Khi đã biết chu vi, ta chỉ cần chia cho 4 để tìm ra độ dài một cạnh.
a = P / 4
Ví dụ: Một hình thoi có chu vi là 60cm. Tính độ dài một cạnh của hình thoi.
Lời giải: Áp dụng công thức, độ dài một cạnh của hình thoi là: a = 60 / 4 = 15 (cm).
Dạng 3: Tính chu vi khi biết độ dài 2 đường chéo (Quan trọng)
Đây là dạng bài tập nâng cao hơn, đòi hỏi bạn phải vận dụng định lý Pytago. Khi hai đường chéo của hình thoi cắt nhau, chúng tạo ra 4 tam giác vuông bằng nhau. Mỗi cạnh của hình thoi chính là cạnh huyền của các tam giác vuông đó.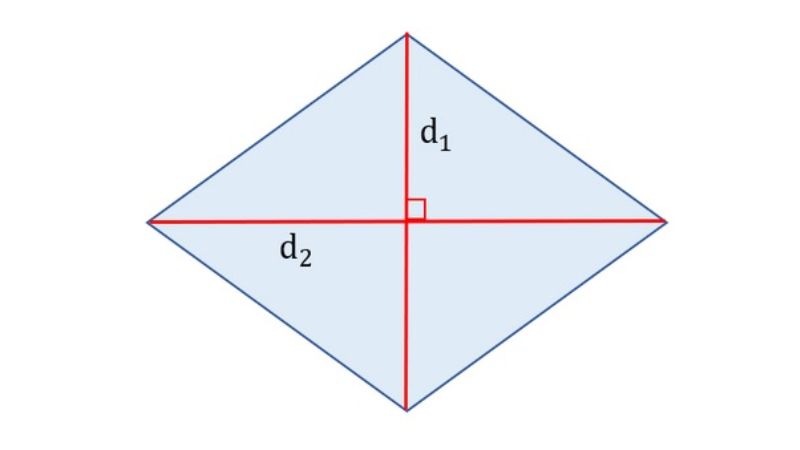
Bước 1: Tìm độ dài hai nửa đường chéo. Gọi độ dài hai đường chéo là d1 và d2.
Bước 2: Dùng định lý Pytago để tính độ dài cạnh (a).
a² = (d1/2)² + (d2/2)²
=> a = √[(d1/2)² + (d2/2)²]
Bước 3: Tính chu vi.
P = a x 4
Ví dụ: Tính chu vi của một hình thoi, biết độ dài hai đường chéo lần lượt là 16cm và 30cm.
Lời giải:
- Nửa độ dài đường chéo thứ nhất là: 16 / 2 = 8 (cm).
- Nửa độ dài đường chéo thứ hai là: 30 / 2 = 15 (cm).
- Áp dụng định lý Pytago, độ dài cạnh của hình thoi là: a = √(8² + 15²) = √(64 + 225) = √289 = 17 (cm).
- Vậy chu vi của hình thoi là: P = 17 x 4 = 68 (cm).
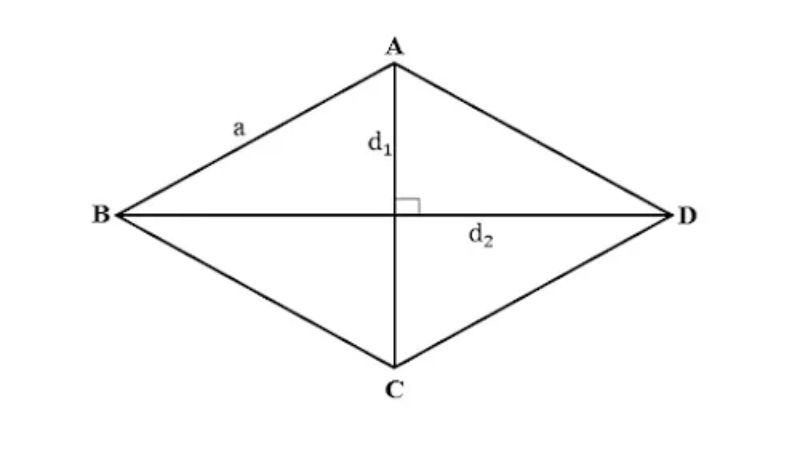
Kiến thức mở rộng: Công thức tính diện tích hình thoi
Bên cạnh chu vi, diện tích cũng là một thông số quan trọng. Dưới đây là 2 công thức tính diện tích hình thoi phổ biến nhất:
1. Tính diện tích qua hai đường chéo:
S = ½ x (d1 x d2)
Trong đó d1 và d2 là độ dài hai đường chéo.
2. Tính diện tích qua chiều cao và cạnh đáy:
S = h x a
Trong đó h là chiều cao và a là cạnh đáy tương ứng.
Một số bài tập vận dụng về chu vi hình thoi (có lời giải)
Hãy cùng thực hành với các bài tập dưới đây để củng cố kiến thức nhé!
Bài 1: Tính chu vi hình thoi có cạnh dài 5.6cm.
Đáp án: P = 5.6 x 4 = 22.4 cm.
Bài 2: Một mảnh vườn hình thoi có chu vi là 80m. Hỏi độ dài cạnh của mảnh vườn là bao nhiêu?
Đáp án: a = 80 / 4 = 20 m.
Bài 3: Một tấm kính hình thoi có độ dài hai đường chéo là 12cm và 16cm. Tính chu vi của tấm kính đó.
Đáp án: Độ dài cạnh a = √[(12/2)² + (16/2)²] = √(6² + 8²) = √(36 + 64) = √100 = 10 cm. Chu vi tấm kính là P = 10 x 4 = 40 cm.
Bài tập ứng dụng công thức tính diện tích của hình thoi
Bên cạnh bài tập tính chu vi hình thoi, bạn cần tìm hiểu một số bài tập giúp bạn hiểu hơn về cách tính diện tích của hình thoi:
Bài 1
Cho 1 khu đất có hình thoi và 2 đường chéo của khu đất có tổng độ dài bằng 400cm. Trong đó chiều dài của đường chéo đầu tiên sẽ bằng 3/5 chiều dài của đường chéo thứ 2. Hãy tính S của khu đất này?
Đáp án:
Số phần được phân ra từ hai đường chéo của khu đất là 3 + 5 = 8 phần
Chiều dài của đường chéo 2 = (400/8) x 5 = 250cm
Chiều dài của đường chéo đầu tiên = 400 – 250 = 150cm
S của hình thoi = (250.150)/2 = 18750 cm2
Bài 2
Cho 1 khu đất dạng hình thoi bao gồm chiều dài của đường chéo 1 bằng 20m, chiều dài của đường chéo 2 bằng 3/4 chiều dài của đường chéo 1. Người nông dân trồng khoai lang trong khu đất và từng m2 này sẽ thu được khoảng 5kg khoai lang. Vậy người nông dân này thu được mấy kg khoai lang?
Đáp án:
Chiều dài của đường chéo 2 = (20/4) x 3 = 15m
S của khu đất có dạng hình thoi = (20 x 15)/2 = 150 m2
Số kg khoai lang thu được trong khu đất = 150 x 5 = 750kg
Bài 3
Cho 1 hình thoi tên ABCD với điểm O được coi là giao điểm 2 đường chéo. Cho biết S hình thoi này bằng 60cm2 cùng cạnh AC bằng 10cm. Vậy hãy tính chiều dài của cạnh hình thoi này?
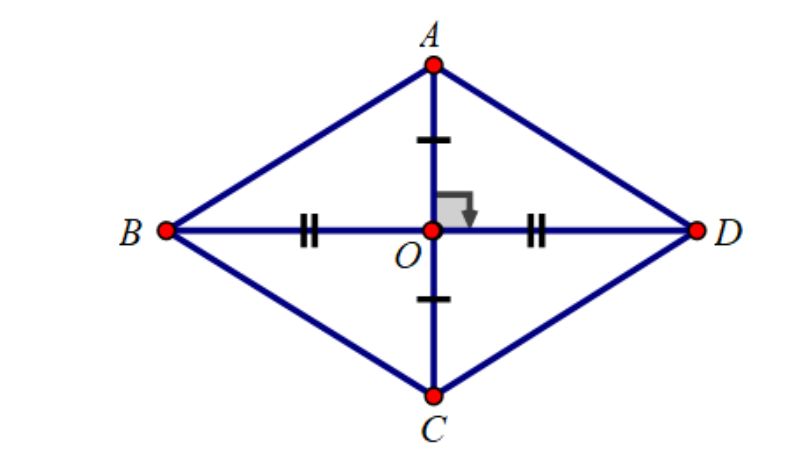
Đáp án:
S của hình thoi = 1/2 x AC x BD
Từ đó suy ra BD = (2.S) : AC = (2 . 60) : 10 = 12cm
Dựa trên tính chất hình thoi thì ta có O được coi như trung điểm cạnh BD, AC.
Suy ra cạnh OA = 1/2 x AC = 1/2 x 10 = 5cm
→ Cạnh OB = 1/2 x BD = 1/2 x 12 = 6cm
Ta tiếp tục sử dụng định lý của Pitago vào trong tam giác tên AOB và được:
AB^2 = OA^2 + OB^2 = 5^2 + 6^2 = 61 → Cạnh AB bằng 7.81cm (chiều dài các cạnh của hình thoi tên ABCD ở trên)
Như vậy bài viết đã cung cấp kiến thức về chu vi hình thoi và diện tích hình thoi cho mọi người tìm hiểu. Đặc biệt là các bạn học sinh phải nắm chắc công thức này và giải các bài tập liên quan thường xuyên để làm các bài thi tốt hơn. Hiện nay các dạng toán hình học đều có đề cập tới hình thoi và các công thức của nó.
Tham khảo bài viết liên quan: