Bộ công thức tổ hợp, chỉnh hợp, hoán vị luôn khiến các bạn học sinh THPT dễ nhầm lẫn giữa các định nghĩa và công thức tính toán chính xác. Trong quá trình học thì các bạn phải phân biệt rõ ba loại công thức này thì mới làm bài tập và bài thi hiệu quả. Bài viết sau sẽ giới thiệu rõ hơn về công thức chỉnh hợp, tổ hợp, hoán vị cho các bạn tìm hiểu thật chuẩn.
Hoán vị trong toán học và các dạng thường gặp
Đầu tiên chúng ta sẽ tìm hiểu về hoán vị và những kiểu hoán vị hay gặp nhất:
Định nghĩa hoán vị
Nếu giải thích mỗi từ thì các bạn có thể coi từ “hoán” có nghĩa là “hoán đổi” và từ “vị” có nghĩa là “vị trí”. Chẳng hạn chúng ta có tập hợp các số X bao gồm số lượng “n” phần tử khác nhau (điều kiện là n ≥ 0). Như vậy thì từng kiểu sắp xếp các phần tử thuộc tập hợp X theo một thứ tự cụ thể được coi là 1 hoán vị của “n”. Thường thì số lượng hoán vị của “n” sẽ được viết ký hiệu ngắn gọn là “Pn”.

Hoán vị có mấy dạng thường gặp?
Hiện nay có 3 loại thường gặp đó là:
Hoán vị dạng lặp
Đây là dạng hoán vị mà khi chúng ta cho số lượng “n” đối tượng và trong số đối tượng đó có “ni” các đối tượng thuộc loại “i” đồng thời có những kiểu cấu trúc y hệt nhau. Hiểu đơn giản thì với từng kiểu sắp xếp thứ tự n phần tử thì trong đó sẽ có khoảng “n1” phần tử sẽ là “a1, n2” phần tử sẽ là “a2”… và có “nk” phần tử sẽ là “ak” (n1 + n2 + n3 +…..+ nk = n) được sắp xếp theo thứ tự ngẫu nhiên và đó được coi là một hoán vị dạng lặp có cấp là “n” với kiểu (n1, n2,…, nk) thuộc “k” phần tử.
Từng kiểu sắp xếp bao gồm thứ tự là “n” phần tử đã cho thì đó gọi là 1 hoán vị dạng lặp thuộc “n”.
Công thức dùng để tính toán loại hoán vị dạng lặp sẽ là:
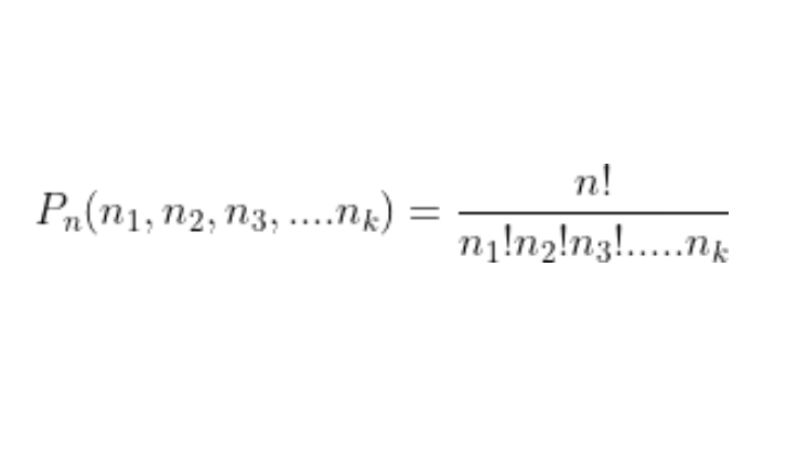
Trong đó, ta có:
- “Pn” là hoán vị dạng lặp có cấp “n” với kiểu (n1,n2,…, nk) của số lượng “k” phần tử.
- n = n1 + n2 +…..+ nk: Số phần tử.
- “n1” là số lượng phần tử “a1” có cấu trúc giống nhau
- “n2” là số lượng phần tử “a2” có cấu trúc giống nhau.
- “nk” là số lượng phần tử “ak” có cấu trúc giống nhau.
Hoán vị dạng vòng
Đây là dạng hoán vị bao gồm những phần tử ở bên trong của hoán vị có thể tạo ra 1 vòng cùng với số lượng phần tử là k lớn hơn 1 và “k” phải là một số nguyên. Công thức tính hoán vị dạng vòng là:
Q(n) = (n-1)!
Hoán vị dạng đồng nhất
Hay nhiều người còn gọi là hoán vị đổi chỗ, đây là kiểu hoán vị có phần tử đầu tiên với phần tử đầu tiên, phần tử 2 với phần tử 2… Nghĩa là thực tế thì không có sự đổi chỗ giữa những phần tử này.
Tổ hợp, chỉnh hợp là gì?
Trước khi tìm hiểu công thức tổ hợp, chỉnh hợp thì mọi người phải tìm hiểu khái niệm sau đây:
Định nghĩa tổ hợp
Tổ hợp là phương pháp mà chúng ta chọn các phần tử trong nhóm lớn mà không cần phải phân biệt về mặt sắp xếp thứ tự. Ở một số trường hợp thì các bạn được đếm cả số lượng tổ hợp. Tổ hợp có dạng chập “k” của số lượng “n” phần tử nghĩa là số các nhóm bao gồm “k” phần tử lấy ra từ nhóm “n” phần tử và giữa nó chỉ có sự khác biệt về những thành phần trong cấu trúc chứ chưa xem xét thứ tự của những phần tử.
Với từng tập hợp con bao gồm số lượng “k” phần tử trong tập hợp lớn bao gồm số lượng “n” phần tử (với n>0) thì được coi là tổ hợp gồm chập “k” của số lượng “n” phần tử.
Định nghĩa chỉnh hợp
Đây là phương pháp mà chúng ta chọn các phần tử trong 1 tập hợp lớn hơn mà vẫn phân biệt về thứ tự sắp xếp. Điều này ngược lại với dạng tổ hợp là nó không cần sự phân biệt về mặt thứ tự.

Ta có chỉnh hợp gồm chập “k” của “n” sẽ là 1 tập hợp con của 1 tập hợp lớn S bao gồm số lượng “n” phần tử. Tập hợp con này sẽ bao gồm số lượng “k” phần tử thuộc tập S và tuân theo một thứ tự sắp xếp.
Bộ công thức tổ hợp, chỉnh hợp, hoán vị đầy đủ nhất kèm ví dụ
Sau đây là bộ công thức tổ hợp chỉnh hợp, hoán vị đầy đủ nhất trong Toán học:
Công thức tính toán chỉnh hợp
Theo khái niệm đề cập ở trên thì chúng ta có số lượng chỉnh hợp chập “k” của 1 tập hợp bao gồm “n” phần tử (1≤ k ≤ n) sẽ được tính theo công thức:

Ví dụ minh họa 1: Chúng ta có mấy cách sắp xếp 3 bạn Hoàng, Hiếu, Hưng vào 2 chỗ ngồi đã có sẵn?
Đáp án:

Ví dụ minh họa 2: Có mấy số bao gồm 04 chữ số hoàn toàn khác được thiết lập từ những chữ số là 1,2,3,4,5,6,7.
Đáp án:
Chúng ta sẽ có từng số bao gồm bốn chữ số hoàn toàn khác được thiết lập từ việc lấy ra 04 chữ số của tập hợp A gồm các phần tử là 1, 2, 3, 4, 5, 6, 7 rồi sắp xếp nó theo những thứ tự cụ thể. Từng số này sẽ được xem là 1 chỉnh hợp có chập 04 của 07 phần tử.
Suy ra số lượng số tự nhiên được tạo ra từ tập hợp trên là 840 số.
Công thức tính toán tổ hợp
Khi nhắc đến công thức tổ hợp, chỉnh hợp, chúng ta sẽ có công thức tính tổ hợp gồm chập “k” của số lượng “n” phần tử (1≤ k ≤ n) là:
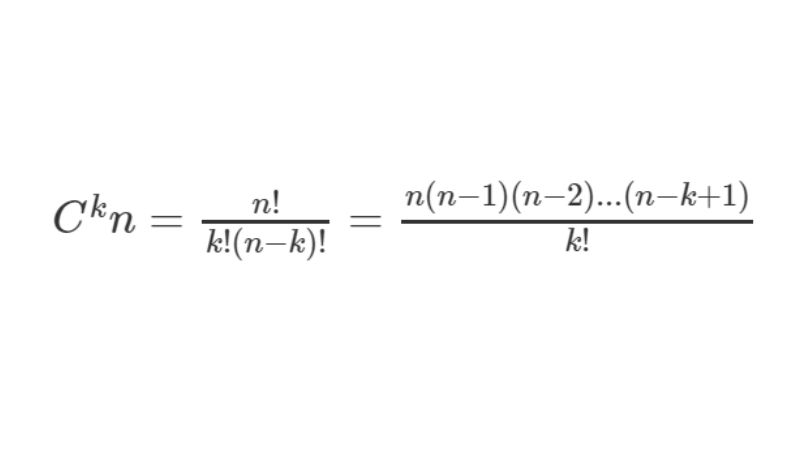
Trong đó “kn” có đáp án là 0 khi k > n.
Ví dụ minh họa: Ông B có chơi với tổng cộng 11 người. Nhưng ông B muốn gửi lời mời cho 05 người trong số họ đi ăn cùng. Trong số 11 người bạn đó thì có 02 người là không muốn đi gặp mặt. Vậy ông B sẽ có mấy cách để mời họ đi ăn?
Đáp án:
Ông B chỉ có thể mời một trong hai người bạn và ông sẽ mời thêm khoảng 4 người bạn trong 9 người bạn kia. Như vậy ta có:
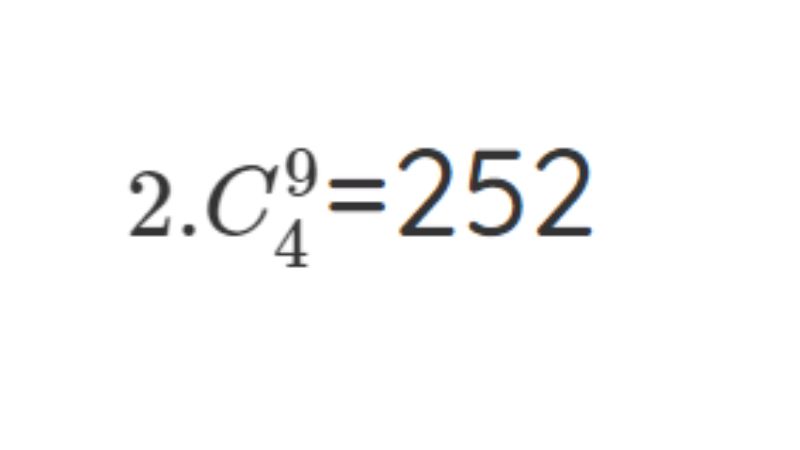
Ông B không gửi lời mời cho hai người bạn kia mà chỉ gửi lời mời cho 5 người trong chín người bạn. Như vậy ta có:
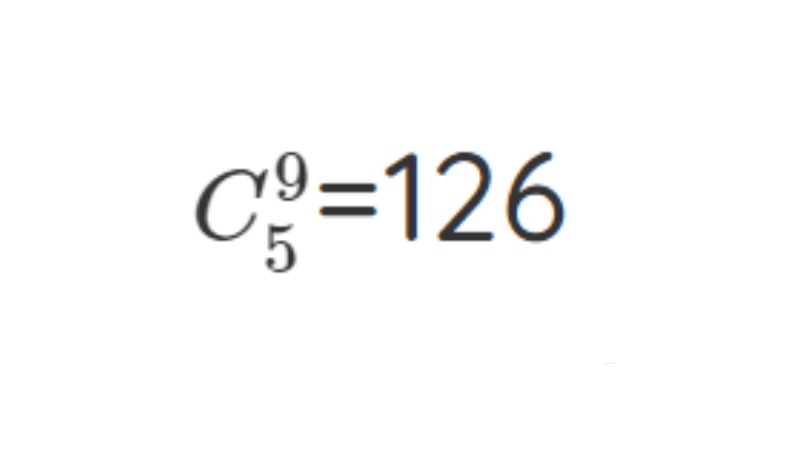
Tổng cộng là ông B sẽ có 328 cách để mời.
Công thức tính toán hoán vị
Công thức để tính toán hoán vị khá đơn giản. Nếu chúng ta có một tập hợp bao gồm số lượng “n” phần tử (điều kiện n> 0) thì ta có công thức tính hoán vị của số lượng “n” phần tử như dưới đây:
Pn=n!
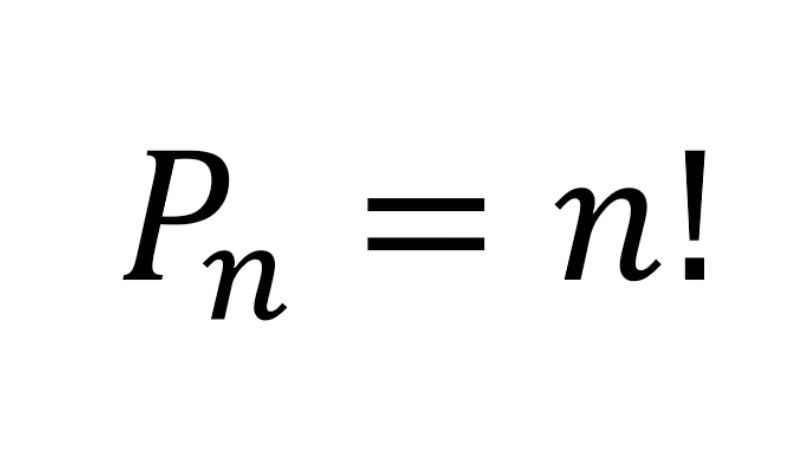
Bài tập minh họa 1: Cho 1 tập hợp tên là A gồm 5 số là 3, 4, 5, 6, 7. Dựa trên tập hợp này thì các bạn có thể thiết lập được mấy số tự nhiên bao gồm 5 chữ số khác nhau?
Đáp án: Bạn có thể áp dụng công thức tính hoán vị là Pn=n!. Như vậy ta có P5 = 5! và đáp án là 120 số.
Bài tập minh họa 2: Các bạn hãy tính toán số kiểu sắp xếp cho 10 bạn thành 1 hàng theo chiều dọc?
Đáp án:
Từng kiểu sắp xếp cho 10 bạn thành 1 hàng theo chiều dọc chính là một kiểu hoán vị của 10 phần tử. Như vậy, số kiểu sắp xếp 10 bạn thành 1 hàng dọc đó là P10 = 10!
Mối quan hệ của chỉnh hợp, tổ hợp, hoán vị trong toán học
Qua khái niệm và những công thức tổ hợp, chỉnh hợp, hoán vị ở trên thì chúng ta có thể thấy nó có mối quan hệ chặt chẽ với nhau. Cụ thể là 1 chỉnh hợp có chập “k” của “n” phần tử sẽ được thiết lập bằng việc tiến hành hai bước sau:
- Bước 1: Bạn lấy một tổ hợp có chập “k” của “n” phần tử.
- Bước 2: Bạn thực hiện hoán vị cho “k” phần tử.
Vì vậy mà các bạn sẽ có công thức dùng để thể hiện mối quan hệ giữa tổ hợp, chỉnh hợp và hoán vị như sau:
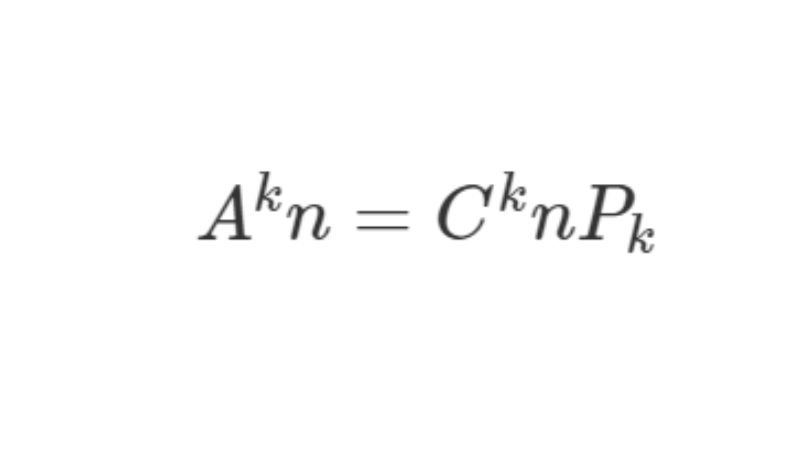
Quy tắc đếm chỉnh hợp, tổ hợp, hoán vị chính xác
Ngoài công thức tổ hợp, chỉnh hợp thì các bạn học sinh nên nắm thêm các quy tắc đếm chỉnh hợp, tổ hợp, hoán vị chính xác như sau:
Quy tắc dùng để đếm các tổ hợp
Ta có 1 tập hợp A gồm số lượng n phần tử với điều kiện là n > 0. Như vậy 1 tổ hợp chập “k” ngẫu nhiên của những phần tử thuộc tập A sẽ là 1 tập con có khoảng “k” phần tử thuộc A, trong đó 0 ⩽ k ⩽ n ; k ∈ N.
Như vậy số lượng tổ hợp sẽ được tính toán dựa trên công thức này: n!(n-k)!
Quy tắc dùng để đếm các chỉnh hợp
Ta có 1 tập A gồm số lượng “n” phần tử với n⩾1. Như vậy 1 chỉnh hợp có chập “k” phần tử phân biệt thuộc A. Trong đó có 1⩽k⩽n, k ∈ N.
Như vậy số lượng chỉnh hợp được tính toán dựa trên công thức này: n!k!(n-k)!
Quy tắc dùng để đếm các hoán vị
Với 1 tập hợp gồm số lượng “n” phần tử phân biệt thì chúng ta sẽ lập được 1 hoán vị của “r” phần tử lấy ra từ tập hợp như sau:
- Lấy phần tử thứ nhất thì ta sẽ có tổng n cách;
- Lấy phần tử thứ 2 thì ta sẽ có n-1 kiểu sắp xếp hoán vị;
- ….
Tương tự khi ta lấy phần tử thứ r trong tập hợp thì ta có r-1 kiểu sắp xếp hoán vị:
- Trường hợp mà r = n thì ta sẽ có công thức đếm số lượng hóa vị khác nhau được lập từ n phần tử. Đó là: P(n) = n!
- Trường hợp mà r < n thì số hoán vị sẽ được đếm theo công thức này: P(n,r)= n!(n-r)!
Bài tập minh họa cho công thức tổ hợp, chỉnh hợp, hoán vị
Sau khi nắm được công thức tổ hợp chỉnh hợp, hoán vị thì các bạn có thể xem một vài bài tập minh họa như sau:
Bài tập 1
Đề thi môn toán của lớp 12 ở một trường THPT gồm 2 loại đề trắc nghiệm và tự luận. Từng học sinh khi dự thi phải làm 2 đề thi bao gồm 1 trắc nghiệm và 1 tự luận. Trong đó có 12 đề tự luận và 15 đề trắc nghiệm. Vậy hỏi từng học sinh sẽ có mấy cách để chọn để thi?
Giải:
Ta sẽ có số cách để chọn một đề tự luận là: 12 cách và số cách để chọn một đề trắc nghiệm sẽ là 15 cách. Vì vậy 1 bạn học sinh phải thực hiện song song cả hai đề. Cho nên sẽ có tất cả là 12 x 15 = 180 cách để chọn đề thi.
Bài tập 2
Ta có một tập hợp A bao gồm các chữ số là 1, 2, 3, 5, 7, 9:
a. Từ tập hợp trên có thể thiết lập được mấy số tự nhiên bao gồm 04 chữ số từng đôi một khác nhau.
b. Từ tập hợp trên có thể thiết lập được mấy số tự nhiên chẵn bao gồm 05 chữ số từng đôi một khác nhau.
Giải:
a. Ta gọi số tự nhiên 04 chữ số là n = a1a2a3a4. Để có được số n như vậy thì chúng ta phải chọn song song các số a1, a2, a3, a4. Trong đó ta có:
- a1 có tổng cộng 6 cách để chọn.
- a2 có tổng cộng 5 cách để chọn.
- a3 có tổng cộng 4 cách để chọn.
- a4 có tổng cộng 3 cách để chọn.
Như vậy thì chúng ta có tổng cộng là: 6 x 5 x 4 x 3 = 360 số n muốn tìm.

b. Ta gọi số tự nhiên chẵn bao gồm 05 số là n = a1a2a3a4a5. Trong đó ta có:
- a5 có đúng 1 cách chọn là 2.
- a1 có tổng cộng 5 cách để chọn.
- a2 có tổng cộng 4 cách để chọn.
- a3 có tổng cộng 3 cách để chọn.
- a4 có tổng cộng 2 cách để chọn.
Như vậy thì số n muốn tìm là 1 x 2 x 3 x 4 x 5 = 120 số.
Bài tập 3
Cho một tập hợp A gồm các số là 0, 1, 2, 3, 4, 5, 6. Từ tập hợp A này có thể thiết lập được mấy số tự nhiên gồm 05 chữ số từng đôi một khác nhau và đảm bảo số 5 và số 2 không đứng bên cạnh nhau.
Giải:
- Tìm ra số tự nhiên có 05 chữ số khác nhau từng đôi một tùy ý:
Số tự nhiên gồm 05 chữ số khác nhau với đôi một tùy ý có dạng là n = a1a2a3a4a5. Trong đó:
- a1 có tổng cộng là 6 cách để chọn (a1 ≠ 0).
- a2 có tổng cộng 6 cách để chọn.
- a3 có tổng cộng 5 cách để chọn.
- a4 có tổng cộng 4 cách để chọn.
- a5 có tổng cộng 3 cách để chọn.
Như vậy thì chúng ta có 6 x 6 x 5 x 4 x 3 = 2169 số tự nhiên.
- Tìm ra số tự nhiên gồm 05 chữ số khác nhau từng đôi một và có số 2 với 5 không được đứng cạnh nhau:
Giả sử ta có số 2 với số 5 là một chữ số a ngẫu nhiên. Chúng ta sẽ tìm số tự nhiên có 04 chữ số:
Trường hợp 1: a1 = a
- a1 có tổng cộng 5 cách để chọn.
- a2 có tổng cộng 4 cách để chọn.
- a4 có tổng cộng 3 cách để chọn.
Như vậy thì chúng ta sẽ có 5 x 4 x 3 = 60 số.
Trường hợp 2: a1 ≠ a nên:
- a1 có tổng cộng 4 cách để chọn (Vì a1 ≠ 0,2,5).
- giả sử a2 = a thì có 3 vị trí cho số a.
- a3 có tổng cộng 4 cách để chọn.
- a4 có tổng cộng 3 cách để chọn.
Như vậy ta sẽ có 4 x 3 x 4 x 3 = 204. Mà số 2 và số 5 có thể hoán đổi vị trí cho nhau. Vì thế nên suy ra ta có: 204 x 2 = 408 số.
Theo yêu cầu bài toán thì: 2160 – 408 = 1572 cách.
Qua những bài tập trên, các bạn có thể hiểu cách áp dụng các công thức trong toán học. Đó là công thức tính chỉnh hợp, tổ hợp, hoán vị trong các bài toán cụ thể. Từ đó các bạn sẽ làm bài tập nhanh chóng và tiếp thu kiến thức nhanh hơn.
Công thức tổ hợp, chỉnh hợp, hoán vị là kiến thức cơ bản ở THPT. Công thức này xuất hiện trong một vài đề thi tốt nghiệp THPT trong nhiều năm qua. Vì vậy, các bạn học sinh phải nắm chắc công thức tính tổ hợp, chỉnh hợp trên để thuận tiện cho quá trình mình ôn thi và làm các bài thi quan trọng.
Tham khảo bài viết liên quan:




